Hovedforskjell: En sirkel og ellipse har lukkede buede figurer. I en sirkel er alle punktene like langt fra senteret, som ikke er tilfelle med en ellipse; i en ellipse er alle punktene i forskjellige avstander fra sentrum.
Matematisk er en sirkel en stor form innen geometri og dens definisjonstilstander: En sirkel er en form med alle punkter i samme avstand fra sentrum. Den er navngitt av sentrum. Noen virkelige eksempler på en sirkel er hjul, middagsplate og (overflaten av) en mynt.
Ordet ' sirkus ' kommer fra det greske begrepet ' kirkos ', som er en metates av homerisk gresk og betyr ' hoop ' eller ' ring '. Sirkelen har vært kjent før innspilt historie. Solen og månen er naturlige eksempler på en sirkel, mens selv en kort stilk blåser i vinden, danner form av en sirkel i sanden. Prinsippen om en sirkel ble brukt i formasjonen av hjul og gir av den prehistoriske mannen. Nå i moderne tid er det utallige varianter av maskineri basert på sirkelformen. Studien av en sirkel og dens utvikling er anvendelig innen matematikk, geometri, astronomi og kalkulator.
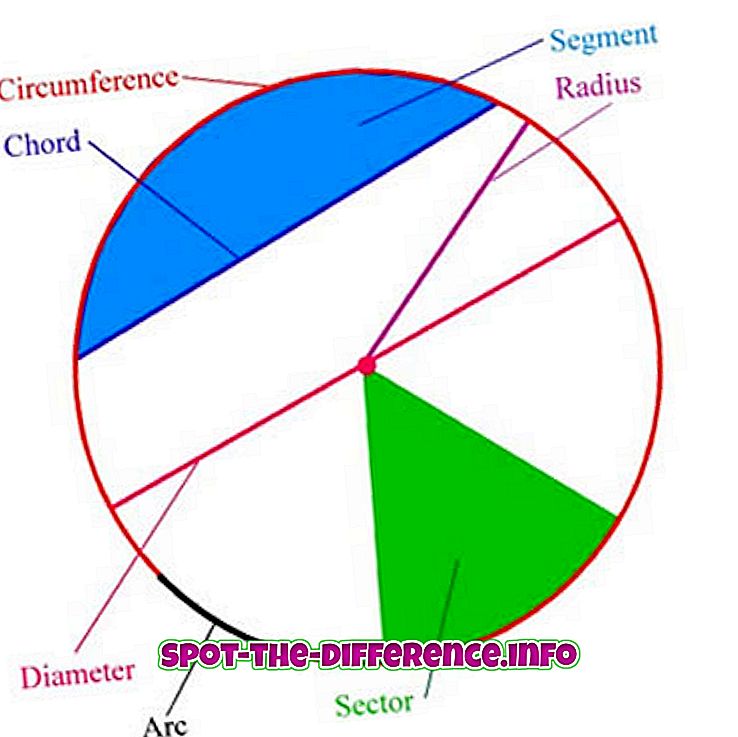
Følgende termer er involvert i sirkelterminologi:
Arc : En hvilken som helst tilkoblet del av sirkelen.
Senter : punktet er like langt fra punktene på sirkelen.
Radius : Et linjesegment som kommer i midten av sirkelen til et hvilket som helst punkt på selve sirkelen; eller lengden på et slikt segment, som er en halv diameter.
Diameter : Et linjesegment hvis endepunkter ligger på sirkelen og som passerer gjennom senteret; eller lengden på et slikt linjesegment, som er den største avstanden mellom noen to punkter på sirkelen. Det er et spesielt tilfelle av et akkord, nemlig det lengste akkordet, og det er to ganger radiusen.
Sirkulerer e: lengden på en krets langs sirkelen.
Akkord : Et linjesegment hvis endepunkt ligger på sirkelen.
Tangent : En parallell rettlinje som berører sirkelen på et enkelt punkt.
Halvcirkel e: en region avgrenset av en diameter og en bue som ligger mellom diameterens endepunkter. Det er et spesielt tilfelle av et sirkulært segment, nemlig den største.
Sirkulær sektor : En region som er begrenset av to radius og en bue som ligger mellom radiene.
Matematisk er en ellipse en vanlig form innen matematikk. Dens definisjon sier: En buet linje danner en lukket sløyfe, hvor summen av avstandene fra to punkter (foci) til hvert punkt på linjen er konstant. Eksempler på virkelige eksempler på en ellipse er: en hula hoop, et glass vann og en enkel middagplate når den er vippet for å se i en vinkel.
Apollonius av Perga ga navnet 'ellipse' i hans Conics, som legger vekt på kobling av en kurve med anvendelse av områder. Det er en kurve på et fly som omgir to fokuspunkter, slik at en rett linje trukket fra et av fokuspunktene til et hvilket som helst punkt på kurven og deretter tilbake til det andre fokuspunktet, har samme lengde for hvert punkt på kurven. Dens form er representert ved sin eksentrisitet, som er vilkårlig nær 1. Studien av ellipse og dens egenskaper er gjeldende innen fysikk, astronomi og ingeniørfag. Banene med planeter med Solen på et av fokuspunktene, månene som kretser om planeter og andre systemer som har to astronomiske legemer, er de generelle eksemplene på elliptiske baner. Formen på planeter og stjerner er ofte godt beskrevet av ellipsoider. Ellipse anses også som den enkleste Lissajous-figuren, dannet når de horisontale og vertikale bevegelsene er sinusoider med samme frekvens.
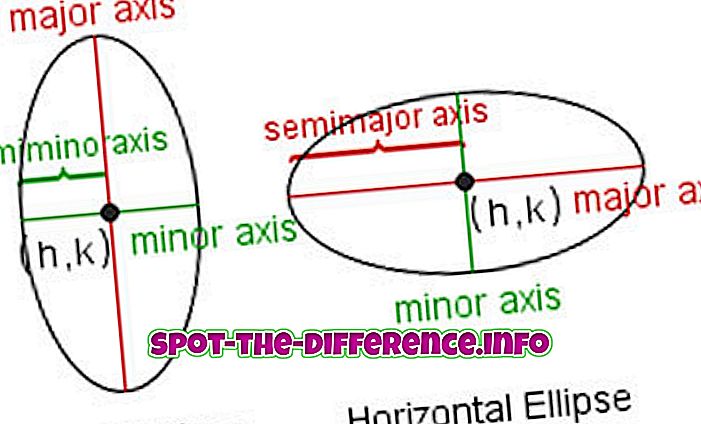
Vilkårene som hovedsakelig er involvert i ellipsens terminologi, er:
Fokus : Avstanden fra sentrum, og uttrykkes i forhold til større og mindre radius.
Eksentrisitet : Ellipseens eksentrisitet (vanligvis betegnet som enten e eller e) er uttrykt i termer ved bruk av flatefaktoren.
Directrix : Det er en linje parallelt med den mindre akse, og med hvilken hvert fokus er tilknyttet.
Latus rektum : Akkorder av en ellipse som er vinkelrett på hovedaksen og passerer gjennom en av dens foci kalles latus endet i ellipsen.
Major / Minorakse : Den lengste og korteste diameteren av en ellipse. Lengden på hovedaksen er lik summen av de to generator linjene.
Semi-major / Semi-minor akse : Avstanden fra sentrum til det lengste og nærmeste punktet på ellipsen. Halve hoved / mindre akse.
Akkorder : Midtpunktene til et sett parallelle akkorder av en ellipse er kollinære.
Omkrets : Det er knyttet til lengden på halvmaxen og eksentrisiteten og er en integrert del av en ellipse.
Sammenligning mellom sirkel og ellipse:
Sirkel | ellipse | |
definisjoner | En sirkel er et rundt planetfigur hvis grense (omkretsen) består av punkter like langt fra et fast punkt (midtpunktet). | En ellipse er en vanlig oval form, sporet av et punkt som beveger seg i et plan slik at summen av avstandene fra to andre punkter (foci) er konstant, eller det oppstår når en kegle er kuttet av et skråt plan som gjør ikke krysse basen. |
variasjoner | Sirkler varierer ikke i form; De forblir i samme form, selv når visningen endres. | Ellipser varierer i form fra veldig bredt og flatt til nesten sirkulært, avhengig av hvor langt unna foci er fra hverandre. |
Radius konsistens | Den har en konstant radius gjennom hele formen. | Den har ikke en konstant radius gjennom hele formen. |
Hovedkomponenter | Sirkelen har en radius, som ligger i sentrum. | Ellipse har to foci, som er i begge ender. |
Område | π × r ^ 2 Hvor er r er radius av sirkelen. | π × a × b Hvor 'a' er lengden på halv-aksen, og 'b' er lengden på halv-mindre akse. |
Standardekvasjoner | (xa) ^ 2 + (yb) ^ 2 = r ^ 2 | x ^ 2 / a ^ 2 + y ^ 2 / b ^ 2 = 1 |
Likhet | Sirkler er de unike formene, hvorfra de andre former kommer fra. | Ellipser oppstår også som bilder av en sirkel under parallell projeksjon og de begrensede tilfeller av perspektivprojeksjon. |