Hovedforskjell: I matematikk brukes en ligning til å indikere likheten mellom to uttrykk. En funksjon derimot er i mye mer kompleks enn en ligning. En funksjon brukes til å betegne et forhold mellom et sett av innganger og et sett med tilsvarende utganger.

En ligning og en funksjon er to av de grunnleggende grunnene til algebra, et emne under matematikk. Begge kan være ganske komplekse i naturen, men i deres grunnleggende form kan de være forvirret som hverandre. Hovedforskjellen mellom en ligning og en funksjon er det faktum at en ligning vanligvis behandler en enkelt inngang, mens en funksjon kan ha mange innganger.

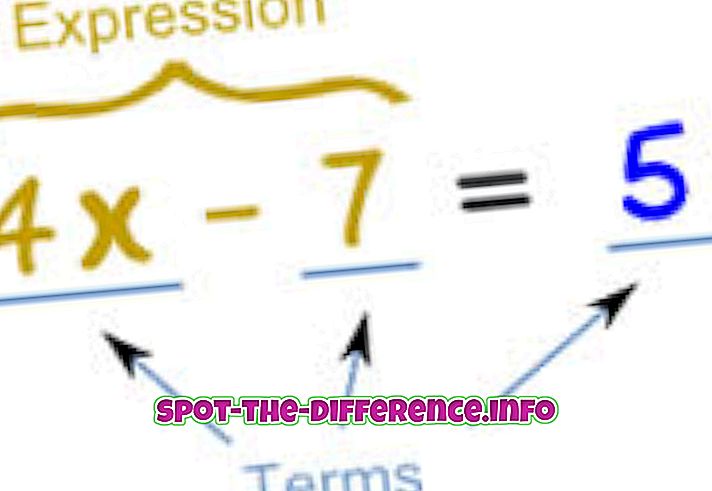
I matematikk brukes en ligning til å angi likheten mellom to uttrykk. I hovedsak er en ligning skrevet som et uttrykk som tilsvarer et annet uttrykk. For eksempel: x + 2 = 5. Dette betyr at det som er x, hvis du legger til 2 til det, vil være lik 5. Derfor kan vi løse ligningen for x, som er 3, som 3 + 2 = 5.

Likninger kan være mer komplekse enn det og kan omfatte mer enn én variabel, for eksempel x, y, z, etc. i en enkelt ligning. For eksempel: 3x + 2y - z = 4. Imidlertid vil hvert alfabet svare til ett tall. I dette tilfellet er x = 1, y = 2 og z = 3.

Derfor

3x + 2y - z = 4 blir

3 (1) + 2 (2) - 3 = 4 som er

3 + 4 - 3 = 4 i hovedsak

4 = 4

En funksjon derimot er i mye mer kompleks enn en ligning. En funksjon brukes til å betegne et forhold mellom et sett av innganger og et sett med tilsvarende utganger. I hovedsak bør en inngang gi en enkelt utgang. En funksjon er et forhold mellom to variabler. For eksempel: f (x) = x + 2. Som i denne funksjonen, uansett, inngangen er, vil den gi deg en enkelt utgang, som vil være inngangen pluss 2. La oss løse denne funksjonen:

Input	Funksjon	Produksjon
x	f (x) = x + 2	f (x)
1	1 + 2	3
2	2 + 2	4
3	3 + 2	5
4	4 + 2	6
5	5 + 2	7

Og så videre…

Funksjoner har ulike anvendelser i matematikk, fysikk, datavitenskap, etc. De kan variere fra en enkel funksjon, som vist ovenfor, til komplekse formler eller algoritmer. En funksjon kan betraktes som en maskin som gir en utgang for en inngang, og at produksjonen på en eller annen måte er relatert til inngangen.

En funksjon har alltid tre deler: inngangen, forholdet og utgangen. Den klassiske måten å skrive en funksjon på er med "f (x) = ...", hvor x betegner inngangen og f (x) angir utgangen.

Som nevnt ovenfor er hovedforskjellen mellom en ligning og en funksjon at en ligning vanligvis har bare ett inngang som vil føre til at uttrykkene er like. Mens en funksjon har forskjellige innganger, som hver vil gi en utgang.