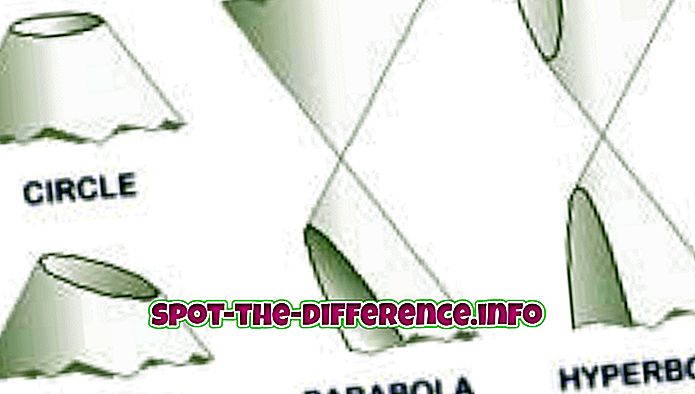
Nøkkelforskjell: En parabola er en konisk seksjon som er opprettet når et fly kutter en konisk overflate parallelt med konusens side. En hyperbola oppstår når et fly kutter en konisk overflate parallelt med aksen.

Parabola og hyperbola er to forskjellige ord, seksjoner og ligninger som brukes i matematikk for å beskrive to forskjellige deler av en kegle. Disse er forskjellige i form, størrelse og ulike andre faktorer i å inkludere formler som brukes til å beregne den. For å forstå dem, la oss først forstå kjeglen og de forskjellige koniske delene.

En konisk del er en kurve som oppnås når et plan skjærer med en kjegle på forskjellige måter. Kuttene som oppnås fra skjæringspunktet er ellipse, sirkel, parabola og hyperbola. Ifølge analytisk geometri defineres konisk som "en plan algebraisk kurve i grad 2." Den populære definisjonen av konisk seksjon inneholder et fokuspunkt, en direkte linje og eksentrisitet. Fokuspunktet og direktelinjene forventes å være i en fast rasjon i en konisk. Forholdet er kjent som eksentrisiteten til den koniske delen. Eksentrisiteten til ellipser, paraboler og hyperboler er forskjellige; ellipser har en eksentrisitet mindre enn 1, parabolas har en eksentrisitet som er lik 1 og hyperboler har en eksentrisitet større enn 1. Det tidligste kjente arbeidet med koniske seksjoner kan dateres tilbake til det fjerde århundre f.Kr. av Menaechmus, som oppdaget en vei å løse problemet med å fordoble kuben gjennom bruk av paraboler.

En parabola er en konisk del som opprettes når et fly krysser med en kjegle. Parabolaer eller paraboler danner 'fra skjæringspunktet til en høyre sirkelformet konisk overflate og et plan parallelt med en genererende rett linje av overflaten.' En annen måte en parabola er opprettet er når et punktpunkt på et fly som er like langt fra fokuset og direktoren skaper en parabola. I algebra brukes paraboler ofte i grafer på kvadratiske funksjoner, ved å bruke formelen y = x ^ 2.

En linje som deler parabolen gjennom midten er kjent som symmetriaksen; denne linjen er også vinkelrett på direktoren og passerer gjennom fokuset. Poengene som ligger på symmetriaksen som krysser parabolen kalles 'vertex'. Avstanden mellom toppunktet og fokuset er kjent som "brennvidde". Paraboler kan åpne i begge retninger, inkludert opp, ned, høyre eller venstre. Også en hovedtrekk ved paraboler er at de er alle de samme, bare forskjellig i størrelse. De kan reposisjoneres og rescaled nøyaktig for å passe alle andre paraboler. Paraboler brukes i forskjellige applikasjoner som billysrelyktorer, design av ballistiske missiler, etc. De spiller også en stor rolle i fysikk, ingeniørfag, matematikk, etc.

Hyperboler er en jevn kurve som oppstår når et plan skjærer sammen med konen parallelt med y-aksen som skaper et kutt langs konusens side. En hyperbola er definert av sine geometriske egenskaper eller ligninger som det er en løsning for. Begrepet "hyperbola" er hentet fra det greske ordet som betyr "overkastet" eller "overdreven". Begrepet antas å være opprettet av Apollonius av Perga, som har bidratt sterkt til studiet av koniske seksjoner.

En hyperbola er kjent for å ha grener som er speilbilder til hverandre og ligner to uendelige buer. Poengene på de to grenene som er nærmest hverandre kalles kryssene. Linjen som forbinder vertikaler er kjent som tverrgående akse eller hovedakse, som tilsvarer hoveddiameteren til en ellipse. Midtpunktet på en tverrgående akse er kjent som hyperbola senter. Ekvationen til en hyperbola er skrevet som x2 / a2-y2 / b2 = 1. Hyperboler brukes i ulike applikasjoner i dagens verden, inkludert stien etterfulgt av skyggen av spissen av en sol, form av en åpen bane; Den brukes som en bu i mange konstruerte bygninger, som ligninger i matematikk og geometri, fysikk, etc.

Hyperboler og paraboler er begge åpne kurver, noe som betyr at de ikke slutter og fortsetter på ubestemt tid til uendelig, noe som ellipser og sirkler ikke kan gjøre.